Reply to Ken Rice (provisional)

Ken Rice posted in reply to Ronan Connolly's summary of his first 3 papers on climate.

---

"Yes, but if there is no greenhouse effect, then the surface temperature would be the non-greenhouse temperature (255 K)."

-- Ken Rice, 2023

---

Short answer:

We get 255k when we assume earth's radiant heat loss is calculated by the Stefan-Boltzmann Law (SBL); without bothering even to add a correction for earth's emissivity. Such that earth cools predominantly by radiative emission throughout its entire atmosphere! (about 79% - at the surface, and 100% at the Top of the Atmosphere).

M = ε × σ × T⁴

M = 1 × 5.67e−08 × 255⁴ = 240 W/m² [ε = 1]

Yet the SBL only applies to an object in a vacuum. Earth's surface is bathed in a gas - its atmosphere. So SBL does not apply to earth's surface.

and if it did, there'd be an emissivity term in the calculation, which Ken and his self-styled 'climate consensus' have erroneously left out too! As I see it: their numbers, even within their own frame of reference, are deliberately wrong! Q: Why?

Long answer:

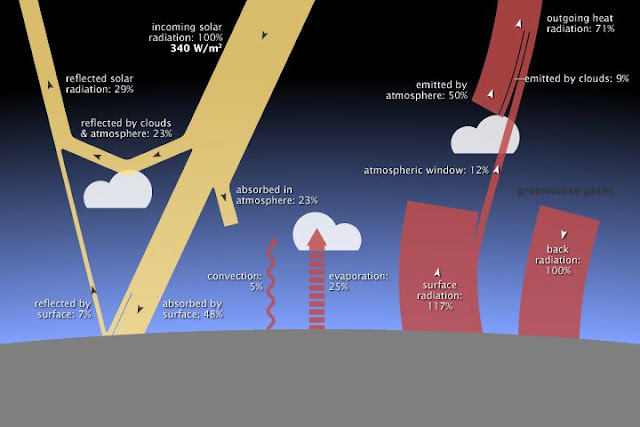
The GHE assumes radiation dominates heat transport throughout ALL earth's atmosphere. For example, two energy balance diagrams (for the surface), written by GHE fans, show:

	K+T1997 W/m²	NASA W/m²	Convective version W/m²
(eb1)	168	163.3	163.3	Incoming solar
(eb2)	324	340.3	1	Incoming infrared 'backradiation'
(eb3)	390	398.2	1	Outgoing infrared
(eb4)	78	88.4	88.4	Outgoing latent heat
(eb5)	24	18.4	74.9	Outgoing convection

Both examples have numbers in the same ball-park. I think Ken and myself agree on two of these numbers: (eb1) sunlight, and (eb4) evapotranspiration. But we disagree on the values for infrared, (eb2), (eb3) and convection (eb5).

We disagree on the two largest values and the smallest one! Evidence tells me the values shown for (eb2), (eb3), and (eb5) are very wrong.

That 255 K figure, is derived by Ken here (Ken Rice, 2017):

"Let’s imagine we have the Earth, but without an atmosphere (or with an atmosphere that is completely transparent). In such a scenario, the surface must radiate back into space – on average – as much energy as it receives from the Sun. If it didn’t, it would either heat up, or cool down, until it did so. If we assume this imaginary Earth has the same albedo as today’s Earth, and orbits today’s Sun, then it would reflect 30% of the incoming sunlight, and would absorb – on average – 240 W/m². It would also, therefore, radiate 240 W/m² and would have an effective surface temperature of 255K"

- KR-2017

Why do I disagree over 255K?

Because I assume:
(a1) Earth warms quickly as radiation travels at the speed of light.
(a2) Earth cools slowly because - in the lower atmosphere: it predominantly cools by convection and conduction, which travel, at best, at the speed of sound. Plus earth has a significant heat capacity. These factors explain why earth's actual temperature = 288K, not 255K.

The greenhouse effect is, of course, the difference between 288 (earth's actual temperature) and 255 = +33C. We're told this +33C warming is due to greenhouse gases.

I disagree with Ken on his 255K number because Ken assumes earth mainly cools by radiation throughout its entire atmosphere. Earth's surface temperature is above 255 K (actually: 288 K), because earth's surface does not cool as quickly as Ken assumes.

(a3) If, like Ken, and his 'climate consensus', friends, one assumes that the Stefan-Boltzmann Law explains 80% of earth's cooling, then one concludes that without a GHE, the surface averages to 255K (or close to that).

My evidence for assumption (a2) is given by Tom Shula in his interview with Tom Nelson regarding how the empirical behaviour of the Pirani gauge precludes a greenhouse effect, GHE, as it's conventionally understood.

Tom Shula disagrees with the Ken, and the 'climate consensus' use of Stefan-Boltzmann Law, SBL, to calculate how earth cools. Their error is to apply SBL out of context. The SBL is ONLY applicable to an object in a vacuum. Even then: ONLY in special circumstances.

For example, Max Planck wrote a book on heat, translated into English in 1914. CHAPTER II, STEFAN-BOLTZMANN LAW OF RADIATION, page 67 begins with a long discussion of an imaginary apparatus for investigating black body radiation. The apparatus which Max Planck describes to elucidate the Stefan-Boltzmann Law reads nothing like the surface of the earth. Planck begins:

"For the following we imagine a perfectly evacuated hollow cylinder with an absolutely tight-fitting piston free to move in a vertical direction with no friction. A part of the walls of the cylinder, say the rigid bottom, should consist of a black body, whose temperature T may be regulated arbitrarily from the outside. The rest of the walls including the inner surface of the piston may be assumed as totally reflecting."

I looked but I can find almost no one, in physics, who measured radiation in a none vacuum!

HELP ME: Please help me here Ken. Please cite some published experiments, done to show the SBL still applies to a surface in a non-vacuum (such as earth bathed in its atmosphere).

Fortunately, the Pirani gauge gives us an experimental setup to investigate heat transport where all of: radiation, convection and conduction can compete to cool a black body, or near black body.

We discover, that at, for example, 65C - a typical temperature used in Pirani gauge measurements, the contribution by radiation is almost negligible when 1 atmosphere of air is present. For each 100W cooling by conduction and convection, ONLY 0.4W of cooling is done by radiation.

The Pirani gauge

So far this - Pirani gauge is the ONLY setup I've seen for measuring radiative output when conduction and convection are also available to cool a body.

---

PS 1:

Does anyone else find it appalling that the Wikipedia entry on the SBL does not mention that the law only applies to bodies in a vacuum?

A suspicious person might conclude there's a global conspiracy of scientists to misrepresent the behaviour of the SBL, in order to con us into believing we're in a "climate crisis" - alternatively - someone who's read Andy West's new book "The Grip of Culture will understand that climate alarm is a cultural entity, in a similar vein to political and religious movements such as Communism or one of the monotheistic religions.". Also: we all know scientists would never do such a thing - conspire! They are paragons of virtue and saintlyness, who would never lie or dissemble - according to the tennants of the climate alarm cultural entity.

PS 2:

Consider the large backradiation value in the energy budgets: 324 W/m² (K+T1997) / 340.3 W/m² (NASA). This number is added to the energy budget to balance out the massive blackbody outgoing radiation previously calculated (390 / 398.2 ). Backradiation is an equation balancing device. It is also the rationale for the GHE! How convenient, to add a GHE by such slight of hand. If no argues against how the SBL is used, then everyone must agree on the backradiation term, so also agree with the GHE calculated by the 'climate consensus'; and so - ultimately agree with the 'climate crisis', and its net zero cure.

PS 3:

As an aside, I should add that both figures provided by NASA and K+T for radiative emissions: 390 W/m², 398.2 W/m² are obviously too high, even when assuming the Stefan-Boltzmann Law does determine earth's surface radiance! The SBL =

M = ε × σ × T⁴

M = emittance (watts); ε = emissivity (unit-less), ε = 1 (black body), ε = 0.92 (average earth surface); σ = Stefan-Boltzmann constant = 5.67 × 10⁻⁸ W/m² × K^-4). , and T = temperature of the emitter. Assuming ε = 0.92, K+T-1997 should've calculated M = 359 W/m². It is ONLY 390 W/m² when one assumes all of earth's surface is a black body emitter - which is obviously a wrong assumption.

Earth's emissivity varies from 0.65 (desert) to 0.95 (water and ice). Given, a third of land is desert, and earth's emissivity is NEVER greater than 0.95; I calculated an average emissivity = 0.92 to get the theoretical: M = 359 W/m²

Oceans	+ Desserts		+ Antarctica	+ The rest
71% × 0.95	+ 4.5% × 0.65	+ 4.5% × 0.75	+ 3% × 0.95	+ 17% × 0.9
Earth's average emissivity =				0.919

Suppose Ken's imaginary average earth surface temperature = 255 K. Then:
M = ε × σ × T⁴
M = 0.92 × 5.67×10e-08 × 255⁴ = 221 W/m²
Ken gets M = 240 W/m²; 8%, or so, too high because he neglects the emissivity term in his SBL
Ken seems to be treating the earth's surface as a black body (assuming its emissivity = 1). It does not. Earth's emissivity is not greater than 0.92.
I cannot even agree with Ken, and his 'climate consensus' allies on how to correctly use the Stefan-Boltzmann Law. I apply the emissivity correction to it. They do not. I doubt they will even justify their assumption that earth's emissivity = 1; when it is obviously not.
LOL. In their energy budget diagram, of 2017, NASA have fraction numbers all over, but they cannot be bothered to correctly apply Stefan-Boltzmann to their own calculations - giving their numbers for OLR and backradiation, at least, an 8% built-in error!
Decades of making stuff up, left them conceited and vainglorious. Or maybe they were already, conceited and vainglorious? That'd explain why the side with The Man's 'net zero', against the people.

Summary:

• Climate consensus energy balance diagrams are completely wrong. In particular the figure for convection (thermals), and infrared radiation (out outgoing, and backradiation) - are totally wrong.
• The figures are wrong because those are the numbers which the Stefan-Boltzmann Law, SBL, gives us.
• But the SBL is invalid because it ONLY applies to objects in a vacuum. Earth's surface is NOT in a vacuum.
• The operation of the Pirani gauge shows what a realistic ratio should be for radiation : convection and conduction, 1 : 250; at earth's surface.
• This changes the outgoing radiation - at the surface - to below 1W/m²; the back-radiation may be close to that too; Convection and conduction will take up the rest of the slack ~ 74.9 W/m²
• A greenhouse gas effect is ONLY required if one assumes radiation dominates cooling in the lower atmostphere. It clearly does not. Remember the wind you feel - that's convection. I repeat: the evidence of the Pirani gauge shows convection dominates radiation when cooling earth's surface.
• BTW: Evapotranspiration is latent heat moved by convection.
• As air thins, higher up in altitude, radiation becomes more important.
• Modellers, such as James Hansen, theorize a window opening to space - at an imaginary altitude where the atmosphere thinned so much that it is too sparse above to reabsorb radiation emitted to space from below. So the radiation escapes earth. Hansen calculated this window to be less than 10km above - still within the tropophere! This is key for him because Hansen's greenhouse effect happens here! (at this imaginary place):

  The basic physics underlying this global warming, the greenhouse effect, is simple. An increase of gases such as CO₂ makes the atmosphere more opaque at infrared wavelengths. This added opacity causes the planet's heat radiation to space to arise from higher, colder levels in the atmosphere, thus reducing emission of heat energy to space. The temporary imbalance between the energy absorbed from the sun and heat emission to space, causes the planet to warm until planetary energy balance is restored.

  -- James Hansen 2011
  
  The location of this supposed window to space - within the tropsophere - is crucial for Hansen's greenhouse effect to work, as he assumes "This added opacity causes the planet's heat radiation to space to arise from higher, colder levels in the atmosphere" If this window were above the troposphere there could not be any greenhouse effect according to Hansen! - because the atmosphere stops cooling at the top of the troposphere where the tropopause begins!
  <- therefore no man-made warming - no need to abandon fossil fuels - no ULEZ - no need for net zero - ...
  It's astounding how tendentious this greenhouse effect is. The special conditions it requires cannot be met.
• I think the evidence from the Pirani gauge shows that if Hansen's window of emission exists - it must be at a higher altitude - above the troposphere!
• At the very top of the troposphere (ToT), air pressure is still above 200 Torr. Radiative cooling does not dominate convection and conduction until the pressure is approaching 0.01 Torr (see Pirani gauge pressure diagram above). At 200 Torr (ToT) - the Pirani gauge diagram shows conduction and convection doing almost as much cooling as it does at 1 atmosphere!
  
  So it looks like James Hansen's greenhouse effect was fiction too.
  
• In the diagram of Earth's Atmosphere (above) James Hansen's imaginary window - where radiation escapes to space - is located at an altitude below the summit of Mount Everest. Where the atmosphere is still over 260 Torr. In the Pirani gauge diagram, atmospheric pressure, 760 Torr intersects the green curve at about 101 Watts. But 260 Torr intesects at about 100 Watts. So convection still dominates. I can't believe James Hansen's imaginary windown exists at an altitude where conduction and covection are still dominant in cooling. I can't believe in a greenhouse effect.
• Q: But if I think this Stefan-Boltzmann Law is unimportant in cooling earth's surface, why did I spend so much time on it above?
  A: Because alarmists misuse it. In particular none of them seem to use a proper term for emissivity! Ken Rice, Kiehl, Trenberth and NASA all miss it. If they cannot be honest about using their most important equation (SBL) - by always including a realistic emissivity term for earth - how can they be honest over anything else?

Hadley Cells

A Hadley Cell is large scale convective movement of air into the tropics which pushes warmer air up. Such warm, moist air releases it's moisture as it cools (which rising in altitude will cause), at the tropics. Hadley and Ferrel Cells explain the trade winds. The Westerlies and Easterlies.

Anyone with any understanding of earth's climate system, knows that convection if the main reason for earth's surface cooling; and the the claim of the IPCC that 79% of earth surface cooling is due to radiative emissions is an incompetent lie.

Citations:

• c1. Max Planck, 1914 (translation), The Theory of Heat Radiation
• c2. K+T1997: Kiehl and Trenberth, 1997
• c3. NASA 2023 : What is Earth’s Energy Budget?
• c4. Ken Rice, 2017
• c5. Tom Shula white paper:
• c6. Tom Shula interview with Tom Nelson
• c7. James Hansen et. al. 2011; 1 Earth's Energy Imbalance and Implications Atmos. Chem. Phys. 2011, 11, 13421-13449. doi:10.5194/acp-11-13421-2011
• c8. Andy West, 2023, The Grip of Culture

Tom Shula clarifies some issues regarding the Pirani gauge and what it says about the "climate crisis"

This is a comment Tom Shula made on his interview by Tom Nelson, explaining how the Pirani gauge precludes the "climate crisis" :

There have been a number of comments/questions regarding the Pirani gauge. Rather than addressing each individually I will attempt explain in more detail here how the heated element in the Pirani gauge serves as a proxy for the surface of the Earth in my exposition. Most of the concepts involved are in the Appendix section of my paper. Also, for reference I will use the chart of the Pirani gauge response. Finally, the Pirani gauge is designed to measure vacuum in a limited range of pressures. There are other devices that operate outside those ranges in applications that need them. We are not concerned with the precision of the gauge. It's value in this exposition is its principle of operation and ability to directly measure the relative contributions of radiation vs. conduction/convection to heat transport in a gaseous environment.

Let's start with the Pirani gauge in a state with a near perfect vacuum in its enclosure. If calibrated as the device represented in the response graph, the controller will provide a current that heats the filament to a specific temperature, in this case the power dissipation is 0.4 milliwatts. That power represents the radiation loss from the filament as well as other losses from junction heating, etc. and may heat the enclosure slightly. At steady state this does not matter, because irrespective of the size of the enclosure the temperature of the filament will remain constant.

In this state, the filament can be expected to emit radiation according to a modified Stefan Boltzmann Law based on its temperature and (typically low by design) emissivity. In this case there is a spontaneous emission of photons from the filament that balances the power input (0.4 mw) from the power supply.

Now, let's introduce some air into the enclosure. We need to look at what is happening at the boundary layer at the filament/air interface. As soon as the gas molecules are introduced, they begin colliding with the filament. Three things happen: 1. Some of the colliding gas molecules pick up energy from the filament at a higher temperature. 2. Removal of the energy from the filament by 1 lowers the temperature of the filament. 3. As a result of 1 and 2, the frequency and average energy of photon emission by the filament is reduced. It is at this atomic level at the boundary where the heat transport begins, and where nature decides the balance.

The gauge controller responds by increasing the power to the filament until it returns to the original temperature, but now in a gaseous environment rather than a vacuum. The additional power is providing a continuous influx of heat capacity (remember this concept) that exactly balances the heat energy that the gas molecules receive from the filament. We know the power input required to maintain temperature under vacuum, and we know the power input required to maintain temperature at pressure. The difference between those two is the power that is being removed by the gas via conduction/convection.

Note that so far there has been no need to take into account enclosure size, enclosure finish/emissivity, filament emissivity, or specific temperature. These can change sensitivity, precision, range, and other operating characteristics of a specific gauge, but the operating PRINCIPLE remains the same. In determining heat transport between a solid surface and a gas, it's what happens at the boundary layer that counts. There is one requirement: the temperature of the filament must be higher than the temperature of the gas, otherwise there would be no net energy transfer from the filament to the gas.

If we are going to consider a particular pressure regime, we might as well look at atmospheric pressure at sea level since that's the place of interest in this exposition. What is the boundary layer at the surface? At atmospheric pressure the molecular mean free path is about 70 nanometers, and the collision rate with a planar surface is about 3 X 1027 collisions/m2-sec. As in the Pirani gauge, conduction at the surface is what triggers heat transport and creates convection. The rate of conduction is proportional to the difference of temperature between the surface and the gas, and INVERSELY proportional to the thickness of the boundary layer. With a mean free path of 70 nm the boundary layer thickness is extremely small, so even a small temperature difference can produce efficient conduction. It also perturbs the radiation output negatively. In the case of a large temperature difference, for example pavement on a very hot day, we can actually see a "mirage" in the distance due to the large lower density convective layer at the surface refracting the sunlight. For smaller temperature differences, it may not be that striking but convection is still occurring. The surface temperature is almost always higher than the air temperature above it. A layman's explanation of why this occurs in soil can be found at: soil temperature

Relative to air, the surface of the Earth whether land or water has a tremendous heat capacity, which is why this has a small effect on the temperature of the surface. This is all that is necessary to demonstrate that the principle of the Pirani gauge applies to the (land) surface of the Earth.

The heating of the surface is from incoming solar radiation. As the solar radiation wanes, the surface will cool, and so the air will cool as well, typically at a faster rate than the surface. The diurnal cycle is dynamic, and it changes throughout the day.

In the case of a water surface (extremely important so not to neglect it) evaporation is occurring on a more or less continuous basis which results in convective transport as well.

Nature has priorities. Flowing water will follow the most efficient path driven by gravity. If something gets in the way, it will go around it or annihilate it. Heat will follow the most efficient path driven by temperature differences. Radiation is natures last resort, when there is no physical medium to transport the heat. When the options of conduction or convection are available, they will always win.

The Stefan-Boltzmann Law at a Non-Vacuum Interface: Misuse by Global Warming Alarmists (reblog)

Reblog: The Stefan-Boltzmann Law at a Non-Vacuum Interface: Misuse by Global Warming Alarmists

One of the significant errors commonly made by the advocates of catastrophic man-made global warming due to CO₂ emissions is the claim by the settled science proclaimers that radiation from a non-vacuum interface is the same as radiation from a surface into a vacuum. This error in the physics of radiation from the Earth’s surface results in an exaggeration of the cooling radiation emitted from the Earth’s surface and contributes to them positing a hugely larger back-radiation from greenhouse gases than can actually occur.

I have previously pointed out that the Stefan-Boltzmann Law actually only tells us the amount of radiation emitted by a surface into a vacuum. A surface in contact with another material will lose energy by other mechanisms, so one must apply the law of Conservation of Energy to determine the actual amount of radiation in many cases of material contact across an interface. In the case of the Earth’s surface, water is evaporated at the surface with a very substantial cooling effect. In addition, air molecules strike the surface and carry away heat gained in collisions with the surface. Despite these obvious problems with an unchanged surface emission of radiant energy into the atmosphere compared to that into a vacuum, the settled science proclaimers have in many cases steadfastly said that I am wrong. OK, so I will try to explain this in greater detail in this post.

Atoms in solid materials such as in soil and rock, are held at distances from one another which are determined by a minimum in the potential energy. The atoms can only be forced closer with the expenditure of energy and they can only be pulled further apart with the expenditure of energy. An electron in orbit about a nucleus will also have motion constrained by a potential energy well. The greater the temperature, the more an atom may move near the potential energy minimum and the more the electron can move in the nucleus-electron potential well. In both cases, positive and negative charges will move with respect to one another. When positive and negative charges are close to one another, but have offset centers of charge, they form a dipole. Because the displacement movements of the charges in the dipoles are small for the temperatures near the Earth’s surface, the results are dipole charges with an oscillating distance between them similar to a mass hanging from a spring in small motion. These are harmonic oscillators and they emit radiant energy. While the interatomic potential energy wells in a liquid are broader than those in a solid material, the same principle applies to liquids. Of course, in either a solid or a liquid, atoms have several nearest neighbors or near neighbors. Multiple harmonic oscillators are interacting.

If a harmonic oscillator in a vacuum is set into motion by a heating process and the heat source is removed, the harmonic oscillation will lose strength as it emits energy into a strengthening radiant energy field. Conversely, an increase in the harmonic oscillation caused by an electromagnetic field, such as the solar insolation acting on the Earth's surface, will decrease the energy in the radiation field. A cooling surface radiating energy will have decreased harmonic oscillator displacements as it pours energy into the electromagnetic field. A surface near 300K will generate infra-red and microwave radiation, though almost all of the energy given off will be in the infra-red radiation range. The generation of a radiant energy field decreases the kinetic energy of the harmonic oscillators in the surface. There is Conservation of Energy between the harmonic oscillators and the electromagnetic field which is generated.

The Stefan-Boltzmann Law tells us how much energy is radiated per unit time into the electromagnetic field of the vacuum:

P = ε σ A T⁴,

where P is the power, ε is the emissivity and characteristic of the surface, σ is the Stefan-Boltzmann constant, A is the surface area of the radiating material, and T is its temperature in Kelvin.

We must remember however that the radiated energy comes from harmonic oscillators. If the surface is a water surface or if it is a soil or a plant with water content and water is evaporated from the surface, we must remember that the energy required to change water from its liquid to its vapor form has to come from somewhere. The Earth’s surface does have considerable water evaporating from it and the latent heat of vaporization for water is very high. Where does this energy come from? Well it comes from the kinetic energy of the oscillating dipoles at temperatures near the average Earth temperature of 288K. As the warm surface materials evaporate water, their harmonic oscillators lose kinetic energy and settle more towards their potential minima except insofar as the energy is replaced by more solar insolation or by heat flow from the subsurface. The oscillation displacements decrease. There is a conservation of energy between the harmonic oscillators and the energy used to evaporate the water. The same is true when the harmonic oscillators warm air molecules that strike the Earth’s surface. Those air molecules take away some of the kinetic energy of the harmonic oscillators.

Consequently, the harmonic oscillators that generate radiation into vacuum will not be able to generate as much radiant energy into the atmosphere. The presence of contacting liquid water and air molecule collisions with the surface remove energy from the harmonic oscillators that generate the radiation field. Consequently, the amount of infra-red and microwave energy emitted from the surface will be less than if that surface were radiating into vacuum. It has to be so because energy is conserved.

This is why it is clear that the Stefan-Boltzmann Law tells us the maximum energy that can be obtained from a warm surface of material. At a vacuum interface, that energy given off will be entirely radiant energy and it will all go into strengthening the electromagnetic field. The Earth’s surface however is taking the same kinetic energy from its many harmonic oscillators and it is partitioning that energy among the processes of generating water vapor, warming colliding air molecules, and emitting radiant energy. The amplitude of the oscillation in the harmonic oscillators decreases as they pour energy into these three loss mechanisms. Energy is thus conserved.

The Kiehl-Trenberth Earth Energy Budget used so prominently in the UN IPCC 4th Report of 2007 made the mistake of not adjusting the Earth's surface radiation downward due to the evaporation of water and the warming of air. Here is that diagram:

It is claimed in this diagram that the Earth's surface at 288K emits 390 W/m² or 114% of the average power incident at the top of the atmosphere and 2.32 times the power absorbed by the surface from solar insolation. The 390 W/m² of surface radiated energy assumes that the Earth’s surface is a black body radiator emitting the same energy it would into vacuum into the atmosphere. As I have explained in my post The Earth Surface Temperature without Greenhouse Gases: The Shade Effect of Infra-Red Active Gases, the Earth’s surface is not a black body radiator. It does not have an emissivity of one as a black body radiator does. It has an emissivity of less than 0.5. But even if it were a black body radiator, energy conservation would require that the emitted radiant energy be (390 – 78 – 24) W/m² or 288 W/m² due to subtracting the energy put into evaporation and thermals. This is 112 W/m² less than they claim is emitted from the surface.

They then make the further mistake of believing that most of that exaggerated surface emitted radiant energy is returned to the surface by greenhouse gases. This makes up much of the 324 W/m² they claim is absorbed by the surface after it had been absorbed in the atmosphere first. The back radiation energy is thus exaggerated hugely by a combination of errors. Among the errors are:

• The belief that the Earth’s surface is a black body radiator with emissivity 1.
• The violation of the Conservation of Energy by failure to subtract the energy used to cause evaporation and to generate thermals from the energy that would be emitted as radiant energy into vacuum.
• The failure to understand the consequences of the high gas molecule collision rates near the surface and the very short mean free path of infra-red radiation which can be absorbed by water vapor and carbon dioxide, as well as their rarity among air molecules. In the lower troposphere, energy is almost entirely transported upward.

The most recent Earth Energy Budget posted by NASA makes the same errors:

This is an incredible comedy of errors for science that has been funded by about $140 billion of hard-earned taxpayer money. It is a comedy of errors with very tragic consequences. Obama and his Democrat Socialist Party are still calling for the destruction of the American economy and the lowering of our standard of living for the supposed purpose of saving the world from catastrophic man-made global warming due to the use of fossil fuels. This disastrous crusade is pursued in the name of this childishly wrong "settled" science. A great many scientists are eagerly participating in this pandering for the goodies handed out by a government eager to exercise still more power while pretending to protect us from a fictional catastrophe. We are ruled by pimps and fools.

The Stefan-Boltzmann Constant is in Error (reblog)

Reblog from: The Stefan-Boltzmann Constant is in Error

It shows about 40 times too much radiation at normal temperatures. (NASA Charts)

The Stefan-Boltzmann constant says that matter emits 459 watts per square meter of infrared radiation at the normal room temperature of 27°C. That's one half of a table top emitting as much energy as five 100 watt light bulbs. Nothing resembling it is happening. Ice supposedly radiates 315 W/m². That's three 100 watt light bulbs per square meter of ice. You could heat a room with a few square meters of ice. Reduce the Stefan-Boltzmann constant by a factor of 40, and the calculated global warming reduces by a factor of 40.

What physicists say is that most things are emitting and absorbing at the same rate, so you don't notice the difference and the above absurdities are facts. They are idiot frauds. A lot of things do not absorb and emit at the same rate including eyes. If half a table top were emitting as much radiation as five 100 watt light bulbs, it would glow so much that it would damage eyes. If it were five heat lamps, it would burn a person's skin.

radiation

The Stefan-Boltzmann constant shows how much radiation is given off by a square meter of any substance at a particular temperature. It is inappropriately applied to the atmosphere where there is no surface and where a transparent gas emits radiation much more readily than a surface does.

W/m² = 5.670373 × 10^-8 × K⁴

Watts per square meter radiation equals a constant times degrees Kelvin to the fourth power.

Simple observations indicate that 20-50 times too much radiation is projected by the Stefan-Boltzmann constant at normal temperatures. The accuracy at higher temperatures is not apparent. The actual curve would be different for each type of molecule. Straight lines should exist between changes in molecular states.

An indication of the error is in the global energy budget which climatologists use. They have to show 79% of the energy leaving the surface of the earth is in the form of radiation because of the Stefan-Boltzmann constant. (See the NASA Energy Budget) A white hot light bulb could not emit 79% radiation without a vacuum environment. Climatologists know that number is preposterous, but it is locked into a narrow range by the Stefan-Boltzmann constant. The actual amount should be 1-3% (estimated maximum). Representing that amount as 2%, in means the Stefan-Boltzmann constant is too high by a factor of 40.

The 1-3% is my estimate of a maximum possibility having worked extensively with temperature effects in electronics; but only a maximum possibility can be estimated through elimination, while the actual would be much less. Radiation is so minuscule that it is ignored in most heat analysis, which means it could not be more than 1-3% of heat loss, while the actual would be much less but cannot be estimated at such a low level. Physicists have not determined what the number should be, which is why they could produce the absurd 79%.

The Stefan-Boltzmann constant is this:

W/m² = 5.670373 × 10^-8 × K⁴

This result is the number of watts per square meter of infrared radiation supposedly given off by matter at a temperature represented by K (degrees Kelvin, which is 273 + °C).

For exactness, this calculation must be adjusted for emissivity, which means variation from the Stefan-Boltzmann constant. For rough, nonreflective materials, it is usually in the range of 75-95%. These variations show the influence of chemistry.

At a normal temperature of 27°C (80°F), the Stefan-Boltzmann constant without emissivity indicates 459 W/m² being radiated.

At the assumed average temperature of the earth (15°C, 59°F), it's 390 W/m².

At the freezing temperature of water (0°C, 32°F), it's 315 W/m².

On a hot day of 37°C (98°F), it's 524 W/m².

On a real cold day of -23°C (-10°F), it's 221 W/m².

It isn't happening. Normal temperature matter is not giving off that much infrared radiation. Virtually everything in physics is in error, unless someone gets the error corrected, which requires a lot more accountability than often exists.

If freezing water were emitting and absorbing the heat of three 100 watt light bulbs per square meter, the heat would interfere with the freezing process. Freezing would be highly finicky and prone to variation.

Physicists have an answer. They say the same amount of radiation is being emitted as absorbed at a stable temperature, so you don't notice the difference. No way. If skin cells were giving off and absorbing 524 W/m² at 98°F, tissue damage would occur between absorption and emission. Energy gets moved around by conduction between absorption and emission of radiation.

Warm clothes would not be warm, if radiation were such a high rate. The insulating effect is largely air space. Air space would be irrelevant at such a high level of radiation. Eskimos use very loose clothes, so a lot of warm air accumulates in them. Warm air would be ineffective if there were a lot of radiation going outward at 524 W/m² and a lot less radiation going inward at 221 W/m² (-23°C).

For example, all electronic components are evaluated for heat to make sure they won't over-heat. Without a fan or air currents for significant convection, which means mostly radiation, almost no cooling occurs. Radiation is in the 1-3% range for warm objects which are cooling by normal convection into the air and closer to zero percent with some air movement such as the constant wind over the surface of the earth.

Yet, climatologists claim radiation is 79% of the heat dissipation from the surface of the earth, which is a cold 15°C average with wind equivalent of a fan blowing.

Not the least reason for the error is that Planck's constant is used to derive the SBC, while there is no Planck's constant, because the whole concept of photons is absurd and admittedly in conflict with the wave nature of light.

The errors in the Stefan-Boltzmann constant are used to rationalize greenhouse gases.

Background Science: Heat causes molecules to vibrate. The vibration of the nuclei sends infrared radiation outward at the same frequency that the nuclei vibrate. More heat creates higher frequency vibrations and higher frequency infrared radiation. Heat also increases the intensity of the radiation.

The Stefan-Boltzmann constant deals with the amount of radiation emitted. With an opaque solid, only the surface molecules emit radiation. Radiation cannot escape from within. That's what opaque means. But a transparent gas such as the atmosphere will obviously allow radiation to escape from within it.

This is why infrared cameras show the atmosphere glowing at night, while solids are black. The depth of the atmosphere allows much more radiation to be emitted than does the surface of solids.

Physicists wrote an equation for the relationship between temperature and the amount of radiation emitted from a surface. Now they apply it to radiation from the atmosphere, which does not have a surface. Square meters are interchanged with cubic meters.

They apply it to all matter—solids and gasses—at all temperatures. It is not logical that radiation would be uninfluenced by molecular forces including bonding and molecular weight. The absurdity of the result at normal temperatures shows that the equation does not properly represent nature.

Anyone would know that radiation will escape from a transparent gas immensely easier than from an opaque solid. Applying the Stefan-Boltzmann constant to the atmosphere says the emission is the same for the atmosphere as for a solid surface. The only reason it is being done is because climatology cannot be reduced to simple math without the Stefan-Boltzmann constant.

Do you think physicists measured the different substances to determine whether they all emit the same? They wrote up a ridiculously simplified equation and applied it to everything. It's a convenience equation. And it's not science. Physicists operate on the engineering principle that if they all use the same twisted ruler, it doesn't matter; and therefore, ultra simplification is called for. In science it matters.

In engineering, it's valid to reduce math to its simplest form; in science, it's not. Yet physicists do; and they reduce physics to engineering in the process. When the basics of physics were being formulated into mathematical equations, about a century ago, the gods of physics had not the slightest ability to evaluate the complexities of the subject, yet they wrote math equations to represent complex phenomena as if nature could be reduced to such simplicity. Their equations are not valid for the complexities of nature. With the Stefan-Boltzmann constant, the reality is that every molecular difference would produce a different constant, yet only one constant is used for all conditions. Engineering thrives on such simplifications, but science is reduced to fraud by it.

---

Here's the problem with the Stefan-Boltzmann constant: Satellite measurements indicate that the sun's energy approaching the earth is 1366 watts per square meter. The amount reflected away is said to be 26%. The amount absorbed into the atmosphere is said to be 16%. (See NASA chart). That's 1366 minus 26% minus 16% = 792 W/m². That's how much radiation would fall on a black asphalt surface at the equator at noon. The Stefan-Boltzmann constant indicates that in a dark basement, a concrete wall at 59°F (the global average temperature) would emit 390 W/m². That's 49% as much radiation emitted from a dark, cold basement as falls on a black surface at the equator. It isn't happening.

---

Night vision equipment shows that there is very little infrared radiation given off by normal temperature matter.

---

You have to realize that physicists pull their equations out of thin air and adapt them to a purpose, usually to expedite technology. It's not a scientific process. Their math is always too simplistic to represent the complexities of nature.

Fake Curve

On the graph below, the solid line is the curve produced by the Stefan-Boltzmann constant. The dotted line shows that there needs to be less radiation given off by normal temperature matter. The difference is the error in the Stefan-Boltzmann constant.

Supposedly, the sun gives off 63 million W/m² at 5,780°K; an incandescent bulb, 4.6 million W/m² at 3,000°K; and normal matter, 459 W/m² at 300°K.

To scale, the Stefan-Boltzmann curve looks like this:

The fourth power on temperature creates an extreme bend in the curve and causes it to go almost straight horizontal at normal temperatures. The horizontal area shows way too much radiation at normal temperatures. The excessive radiation at normal temperatures is used to rationalize greenhouse gases.

Natural effects do not normally have high exponents. The fourth power is probably a result of two errors combined—a squared result (exponent of 2) in heat and temperature relationships, which are assumed to be linear (nonexponential) and a squared result for heat and radiation relationships. But there would not be one curve for heat-radiation relationships. Chemistry and other forces would create too much variation for a single curve, as indicated by emissivity. At extreme temperatures, additional forces probably add more variations.

The linear relationship between heat and temperature is a convenience assumption based upon a closed circle of logic, because the actual measurements are extremely difficult to make and are not realistically being made. The transformation of kinetic energy into heat is represented by Joule's constant, which is given to 5 significant digits. But I showed mathematical proof that the definition of kinetic energy is wrong, which means there is no consistent Joule's constant. The 5 digit number has to be fakery.

The actual curve for heat and radiation relationships looks like it would be S shaped, because a lot of change would occur at normal temperatures. Physicists used a smooth curve resulting from a simple exponent, and as a result, they got too much radiation at normal temperatures.

Due to the exponent of 4 in the Stefan-Boltzmann constant, physicists have 11 times as much radiation being given off by the sun as a light bulb filament but only 1.9 times as much temperature. There could be other forces entering at the temperature of the sun, but this would be a bend in the curve, not an exponential curve. Is twice the temperature of a light bulb filament supposed to produce hydrogen fusion? Not hardly.

The Atmosphere Supposedly adds 33C to the Earth's Surface.

There is an average of 235 W/m² energy leaving the earth. The Stefan-Boltzmann constant says that an object at -19°C emits 235 W/m² black body radiation. But the average earth surface temperature is 15°C. So the earth's surface is 15 + 19 = 34 (rounded to 33) degrees C warmer than it would be without an atmosphere. The atmosphere supposedly keeps the earth's surface warm.

In truth, greenhouse gasses add no heat to the atmosphere, because heat as radiation cools the planet by going around them, not through them. The atmosphere does not need greenhouse gasses to absorb and hold heat, as explained on the page titled Summary in Simple Words.

With a corrected Stefan-Boltzmann constant, the surface of the earth without an atmosphere would emit 235 W/m² at a temperature of something like 50°C, not -19°C. With an atmosphere, the surface average is 15°C. The atmosphere cools, as it should, because it is like a heat sink. This means the atmosphere picks up energy through conduction and convection, which removes heat much faster than radiation alone. Heat sinks (usually made of aluminum) are used for this reason throughout electronics to speed cooling.

Theoretical Concepts

Physicists do not do conception analysis. They despise intuitive logic. Instead, they apply math without regard for the resulting absurdities. The problem is that the math has a high tendency to be wrong, incomplete or over-simplified.

Besides the Stefan-Boltzmann constant resulting in too high of a quantity at low temperatures, the constant is applied to solids and gasses equally, which is absurd. Gasses have a three dimensional surface and low density, which promote the escape of radiation. Therefore, gasses should have a much higher quantity for radiation emission than solids. But there would not be a single constant for gasses, because the chemical composition would determine how radiation escapes, as greenhouse gasses demonstrate.

These points should be quite secondary and not much relevance to global warming, because other factors determine the result. But fake scientists rely heavily upon the Stefan-Boltzmann constant as a rationalization gimmick. They focus upon such claims as radiation leaving the earth at a height of 5km attempting to create a concept in minds of there being a greenhouse effect. Global warming propaganda is all about impressions and a dark pit of unaccountable rationalizations.

Errors in Physics

Why is the Stefan-Boltzmann constant so far off? Observable evidence shows that errors in science, particularly physics, are the maximum which accountability will allow. In physics, there is far less accountability than in biology due to its highly abstract nature.

Consider this simple example. Physicists claim that the Bernoulli principle shows that the pressure of a gas is inversely proportional to velocity, and this allows airplane wings to lift weight due to the high velocity of the air over the top. The velocity is lower under the wing due to less curvature and less distance to travel. You can prove the physicists wrong by blowing on one side of a sheet of paper. Nothing happens. But fold a crease in the paper, and then blow across it. The paper is rapidly pulled by the crease. The crease creates a vacuum pump in the shaded area. High velocity air pulls air molecules out of a shaded area creating a vacuum pump. It is not the velocity alone but the shaded area that creates the force. This means physical shape, not raw velocity, determines the pressure effects of moving air, contrary to the claims of physicists.

This is why an airplane wing needs its bulge near the front instead of the back. If it were raw velocity creating the lift, the bulge would need to be near the back of the wing to increase the surface over which the high velocity air travels. But if it is a vacuum pump creating the lift, the bulge needs to be near the front, so there is more area for the vacuum behind the bulge. The wings have the bulge in front showing that it is the vacuum behind the bulge, not the high velocity in front of the bulge, which does the lifting.

Tim Ball explains the "climate crisis"

"Earlier, I identified what Maurice Strong said was the global problem. “Isn’t the only hope for the planet that the industrialized civilizations collapse? Isn’t it our responsibility to bring that about?”

The question is how do you bring that about? The answer is understood by comparing the industrial nation to a car engine. They both run on fossil fuels. You can stop the engine by stopping the fuel supply. However, if you do that the people will react quickly and negatively – it is politically dangerous. However, you can also stop the engine by plugging the exhaust. Carbon dioxide (CO₂) is a major release from fossil fuels. If you show that it is causing global warming, that is destroying the planet, you justify stopping its production and use. This would shut down the industrialized nation."

-- Tim Ball "Human caused global warming"

PS: Maurice Strong was the first chairman of the UN Environment Programme.